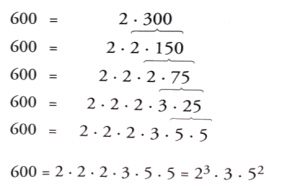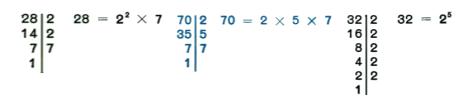Factoring of a number is the number decomposition into prime factors.
If we start from a composite number, by definition we can get your “decomposition” in factors less than the same number, these factors may, in turn, composite numbers or prime. If they are composites, We decompose in the same way in order to decomposition in a prime factors .
Example:

El 12 can be decomposed in 12 = 3 · 4, and in turn 4 = 2 · 2 therefore 12 = 3 · 2 · 2
El 12 can be decomposed too in 12 = 2 · 6, and in turn 6 = 2 · 3 therefore 12 = 2 · 2 · 3
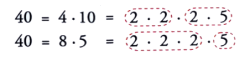
2 ways to obtain factors of 40
whatever the factorization, in the end the prime factors are the same because there are unique possible decomposition in prime numbers.
Knowing this property, the more comfortable procedure to factoring is to use always the primes to split and the quotient to decompose.
¿HOW TO FACTORING?
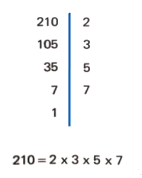
Check if the number is divisible by 2; if it is, we make the Division and test with the quotient again with 2; if it’s not divisible we will see if it’s divisible by 3; and will repeat the same procedure than before. This will be repeated until the quotient it’s 1.
Factors of: 28, 70, 32 y 210:
FACTORING FOR CALCULATING G.C.D. and L.C.M.
Factoring is also used to calculate the greatest common divisor (GCD) and least common multiple (LCM)
gcd of two numbers is the result of the common factors powered to smallest exponent.
lcm of two numbers is the result of the common and not common factors powered to highest exponent.
Example:
Calculate the gcd of 72 and 50
72 = 23 · 32
50=2 · 52
gcd(72,50) = 2
Calculate the lcm of 72 and 50
lcm(72,50) = 23 · 32 · 52 = 1800
We can use factoring to find out if a number is prime, as this will be prime when factoring only has as its prime factors 1 and the same.