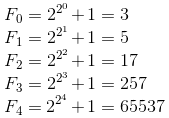The Fermat primes are the Fermat numbers that are prime.
Pierre Fermat conjectured in the sixteenth century that any number like this:
where Fn are the Fermat numbers, are prime numbers for any natural n.
It was not until 1730 when the mathematician Leonhard Euler proved that for n = 5 the number was divisible by 641.
Thus proving Fermat’s conjecture was false.
Despite this, Fermat numbers have some properties studied that relate to prime numbers and hence still further research to learn how many Fermat primes are there and if those are finite.