It’s not an easy task determine if a number is prime or not. Knowing if a number is prime always strongly attracted mathematicians and amateurs who have obtained some partial results, but no one has yet found an exact mathematical formula with acceptable time and algorithmic structure thatresolves this question for all or undefined set of prime numbers.
A number is prime if it’s not multiple or divisible by another number other than itself and unity.
If you want to know if a number is prime, we can test to split by 1,2,3,4 …. up the number, if none of them is divisor of the number then the number is prime.
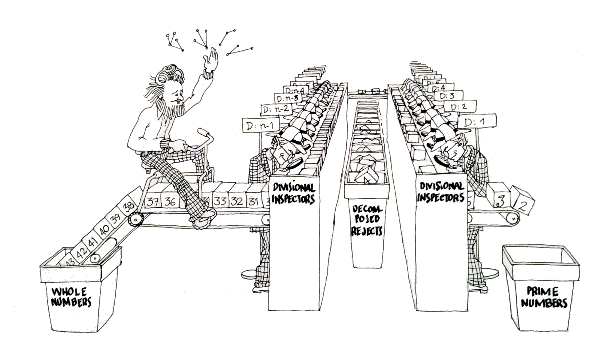
This idea is shown in this drawing is known how “the conway machine” (John Horton), English mathematician at the University of Cambridge, shown in Fig pedaling to operate the machine. The group of inspectors check the number that passes the string is divisible by its assigned divisor and if in afirmative case refuses it into the trash.
The problem is that we have to try as many numbers as the large of the number, so that we can improve the strategy.
We know that if a number is divisible or multiple of another, then any product of that number is too.
Therefore if we divide by a composite number (which is the product of at least one prime), is also divisible by this prime, so:
To know if a number is prime just look if it is divisible only by some prime to number.
But … Do you need to test all the primes up to the number?
Not too, if We look when where are testing in order the primes, we are discarding by order, so the next prime to test multiplied by the previous primes cannot get the number as a result, so we will obtain the number at least with the next prime by multyplying byitself, this means that the search ends with the prime wich has the nearest square to the number without exceeding it, in other words:
To know if a number is prime, simply test if the number is divisible by primes up to its square root.
PRACTICAL CASE
Is 149 prime?
The square root of 149 is 12,2… so it is only necessary test the prime numbers up to 12,2..
We test 2,3,5,7,11
149 : 2 = 74,5.. (not divisible by 2)
149 : 3 = 49,6.. (not divisible by 3)
149 : 5 = 29,8.. (not divisible by 5)
149 : 7 = 21,2.. (not divisible by 7)
149 : 11 = 13,5.. (not divisible by 11)
149 can not be divided by these prime ?numbers then 149 is a prime number.
Is there a formula to tell me exactly if a number is prime?
Yes, the Wilson theorem:
A number n is prime if and only if (n-1)! + 1 is a multiple of n
Example:
Is 7 a prime number?
7 is prime if (7-1)! + 1 is multiple of 7
(7-1)! + 1 = 6! + 1 = (6x5x4x3x2x1)+1 = 5040
Is 5040 multiple of 7?
5040 : 7 = 720 (exact division)
yes 5040 is multiple of 7 then 7 is a prime number.
The problem is when we have big numbers it’s more difficult to calculate because the factorial becomes very large and in last case is not a practical method.
There are more complextests to know the primality of a number but are difficult to push on practice if we are not on computer programming:
PROBABILISTIC
- Solovay-Strassen Test (SS)
- Miller-Rabin Test
- Elliptic Curve Primality Proving
DETERMINISTIC
- Fermat Test(only Mersenne primes)
- Lucas-Lehmer Test(only Mersenne primes)
- Pocklington Prove
- LKL Prove(only Mersenne primes)
In 2002 appeared a deterministic test which ensures a polynomial time if a number is prime or not. It is known as the AKS test and it’s the most important discovery recently about prime numbers.