VERY EASY
A) How many ways can we arrange 12 tiles so that they form a rectangle?
B) Get your calculator and try the following:
What do you get?
C) The A line bus runs every 9 minutes and the B line every 12 minutes. If quite in line at the stop, how much it will take to re-match?
EASY
D) Ana has a deck of cards and can make groups of 2, 3, and 5 without a remainder letter, what are the possible numbers of cards Her can have ?.
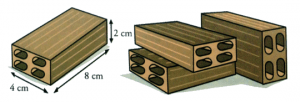
E) We have a type of brick of dimensions:
How many bricks needed to build a cube?
F) A type of cicada has a parasite whose life cycle is between 2, 3 and 5 years, this means that when the season ends and the parasite dies may take 2 3 or 5 years to reappear. What should be the life cycle of the cicada to not match this? (Based on a real case).
MEDIUM
G) Divide the clock into 6 parts so that all its parts add up the same.
E) Participants in a parade can be in ordered in groups of 3, 5 and 25 but can not do in groups of 4 or 9.
What is the number of participants if we know that between 1000 and 1250?
H) Given this imaginary situation of love:
How many laps will have to give each wheel for lovers touch again?.
HARD
I) How to transport the 12 dogs and 18 cats so that all cages have to carry the same number of animals and cages are the largest possible.
Note: No sane enough mix dogs and cats.
J) We have a balance and 8 balls of the same weight except for one that weighs more.
How many weighs have to do to know for sure which is the different ball?
VERY HARD
K) Suppose x is any prime greater to 3. Show that its square gives a remainder of 1 when divided by 12.