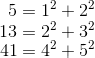Goldbach Conjecture. Christian Goldbach (1690-1764) conjectured that: all number greater than 2 and even is equal to the sum of two primes.
Here are some examples:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
Also known as the strong Goldbach conjecture has been proven using computers to the even numbers up to one hundred million, but has not yet been demonstrated.
In contrast, the Goldbach’s weak conjecture which states that any number greater than 5 and odd is equal to the sum of three primes was recently demonstrated by the Peruvian mathematician Harald Helfgott.
Fermat Conjecture. Pierre de Fermat (1601-1665) conjectured in 1637 that there are no integers verifying the following equation for n greater than or equal to 2
Fermat’s conjecture remained unproven three centuries and a half. In June 1993, the English mathematician Andrew Wiles announced that he had proved Fermat’s conjecture. But his show had some gaps, it took over a year to resolve. Finally, Fermat’s conjecture has been established, becoming the Fermat’s last theorem.
Fermat’s little theorem: 2 ways to express:
- For any a number a and p prime
.
the other way is:
- If p is prime, and a coprime to p then
.
Example:
Fermat’s theorem on sums of two squares Every prime number p can be written as: 
, where x and y are integers if p = 2 or p=1 (mod 4).
{5,13,41} are of 4k + 1 form, or in other words are congruent to 1 mod 4.
Euler’s Theorem (1736) If a and n are coprimes:
is multiple of n.
in the language of the elements Zn is:
where 
is the Euler’s totient, which counts the coprime numbers with n up to n.
Mills’ Constant (1947)
The 
constant generates 
prime numbers for any n natural.
If the Riemann hypothesis is true the value of the constant is = 1,30637788386308069046….
since there is no known way to calculate this constant and it is unknown if the rational number.